How to Read Linear Linear Stata Regression Output
Regression Analysis: Interpreting Stata Backslide Output
Regression Analysis
Regression analysis is a statistical method used past data analysts to estimate the relationship between a dependent variable and independent variable(southward). In our articles on linear regression and logistic regression, we described independent variable(southward) every bit variables we wish to utilise to predict the response variable (dependent variable), while dependent variable as a variable we wish to explain its variation using the contained variable(southward).
Interpreting the findings of regression analysis is an of import skill in data analytics because it can serve every bit a guide for data driven decisions in organizations. In this article, I volition be explaining the regression output of Stata and the interpretation of the different results.
Stata Regression Output
Stata is a statistical software used for data analysis, management and visualization. Its regression output is highly informative and it is one of the most widely used tool for estimating the relationship between dependent variable and independent variable(s).
In this article, we volition be because a randomly generated information with twenty observations, iii independent variables and i dependent variable. 1 of the independent variables is a categorical variable. The data is every bit shown beneath:
.png)
Using Stata to fit a regression line in the data, the output is as shown below:
.png)
The Stata output has three tables and we will explain them one later on the other.
- ANOVA table : This is the table at the top-left of the output in Stata and it is as shown below:
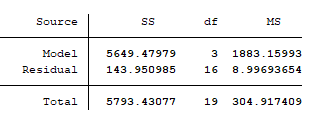
SS is curt for "sum of squares" and it is used to stand for variation. The variance of the target variable comprises of that of the model (explainable variance) and that of the residuals (unexplainable variance). The full SS is the total variation of the target variable around its mean. it is given past:
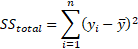
Where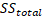 
represents the total variation that the target variable has.
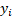is the value of the target variable for a given observation.
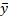is the hateful of the target variable.
On the other paw, SS rest is represents the unexplainable variation of the target variable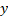 
(the variation of 
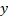around its mean that our model cannot explain or capture). This is the variation of the residual and is given by:
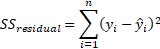
Where 
represents the total variation that the target variable has.
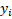is the value of the target variable for a given observation.
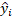is the predicted value of the target variable for a given ascertainment.
The model's sum of squares (explainable variance) would thus be:
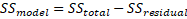
Which is mathematically equivalent to:
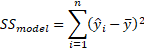
From the output, nosotros can see that out of a variation of 5793.43 in the dependent variable, 5649.48 is explainable by the model, while the remaining 143.95 is unexplainable.
df is the degree of freedom associated with a variance. Degree of freedom is the number of independent values that tin can vary. It is ofttimes given by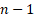 
.
The total degree of freedom is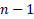 
where 
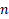is the number of observations in the data.
Since the model estimates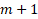 
number of variables (including the intercept), the degree of liberty in the ANOVA tabular array is given past:
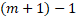
Where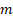 
is the number of predictors (independent variables), the +1 represents the intercept.
The remainder degree of freedom is the difference between the total degree of freedom and the model degree of freedom. It is given by:
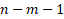
From the output, nosotros run across that the degrees of freedom of the model, and residuals are iii and sixteen respectively, while that of whole data (total) is 19.
ms is the mean of the sum of squares. It is the sum of squares per unit degree of liberty (sum of squares divided by the degree of freedom).
From the output, the mean sum of squares of the model, rest, and total are respectively 1883.16, 8.997, and 304.917.
2. Model fit : This table summarizes the overall fit of the model. Information technology answers the question "how well does the model use the predictors to model the target variable?" . The tabe is every bit shown below:
Number of obs is simply the number of observations used in the regression. Since the information has 20 observations, Number of obs is equal to 20.
F(three, sixteen) is the F-statistics of an ANOVA exam run on the model. The F-statistics is the ratio of the hateful sum of squares (ms) of the model to that of the balance. Information technology measures how the ratio of the explainable mean variance to the unexplainable mean variance is statistically greater than 1. The 3 and 6 merely represents the model's and rest degrees of freedom respectively. To know how well the predictors (taken together as a group) reliably predicts the dependent variable, Stata conducts an hypothesis exam using the F-statistics. The null hypothesis is that the mean explainable variance is same as the mean unexplainable variance. From the tabular array, we see that the mean sum of squares of the model is almost 209.31 times greater than that of the residual.
The Prob > F is the probability of obtaining the estimated F-statistics or greater (the p-value). For a typical alpha level of 0.05, a p-value lesser than 0.05 similar we have in our output, means that we have evidence to reject the null hypothesis and have the alternate hypothesis that the ms of the model is significantly greater than that of the residual. Hence, the predictors of our model reliably predicts the target variable.
R-squared is the coefficient of determinant and it represents the goodness of fit. It is numerically the fraction of the variation in the dependent variable that can be accounted for (explained) by the contained variables. It is given past:
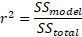
From the output, 97.52% of the variation in the dependent variable are explainable by the model.
Adj R-squared: Since the add-on of more and more predictors tend to increase the R-squared, Adj R-squared tells u.s.a. how much of the variation of the dependent variable is determined by the improver of the independent variables. Adj R-squared is the R-squared controlled for by the number of predictors. It is given by:
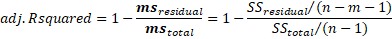
From the output, nosotros can say that after adjusting for the caste of freedom, the coefficient of the determinant is 97.05%
Root MSE is but the standard deviation of the residuals (error term). From the output, we can say that the measure of the spread of the residuals is 2.9995
- Parameter Estimation : This table shows the parameters estimated by the model and their respective statistical significance. In addition to the estimated coefficients, Stata conducts a hypothesis exam using the t-test to detect how each estimated coefficient is significantly different from nix. The null hypothesis for each independent variable is that they have no relationship with the dependent variable hence, they have an estimated parameter of cipher, and that the intercept is zero. The alternate hypothesis is that these coefficients are significantly different from cypher.
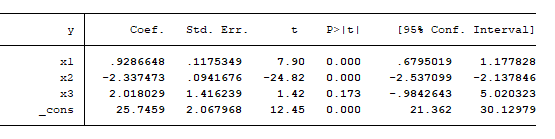
y represents the target variable; x1, x2, and x3 represent the independent variables; and _cons
represent the abiding term (intercept).
Linear Regression
For a linear regression, Coef. Is the approximate of the values of the coefficients of the contained variables, and the value of the intercept. The equation of the model can thus be represented as follows:
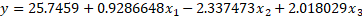
Retrieve that from our linear regression article, nosotros explained that these coefficients are the corresponding partial derivative of the dependent variable with respect to each independent variable and the intercept. That is, they represent the change in the target variable for a unit of measurement increase in the independent variable holding all other factor constant. We interpret these coefficients every bit follows:
- Holding all other factors constant, the value of
volition increase by well-nigh 0.9286648 for a unit increase in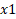 
. - Holding all other factors constant, the value of
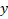will decrease by nigh 2.337473 for a unit increase in 
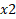. - Holding all other factors constant, the value of
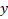will increment by about 2.018029 for a unit increase in 
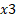. Since 
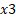is a categorical variable, bold 0 represents female person while 1 stand for male; a unit of measurement increase in 
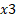is same every bit switch from female (0) to male (i). We tin can thus say that the value of 
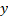increases by about ii.018029 for every unit of measurement switching from female person gender to male or better still; we tin say that belongings all other factor constant, the value of 
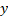for male is ii.018029 more than than that for female. - Belongings all other factors abiding, the value of
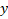is 25.7459 when all the independent variables each have a value of aught.
Logistics Regression
If the dependent variable was categorical, the interpretation would change a niggling. Remember that from our logistic regression article, we showed that a regression model fits a line on the logit of the target variable. Since logit is the natural logarithm of the odd ratio, the odd ratio is thus the exponent of the logit. Think that odd ratio is the ratio of the probability of success to failure i.e. how many times the take chances of failure is the chance of success.
We tin can represent the linear equation as:
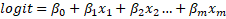
Each of the coefficient is thus the change in logit for a unit change in the independent variable. To translate change in logit, we tin write the modify in logit as:
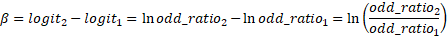
Therefore,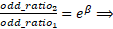 
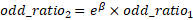
The above however is a ratio of odd ratios. For better interpretability, it is best to interpret the alter in the dependent variable as a fractional change in the odd ratio.
Therefore, the partial change in the odd ratio is:
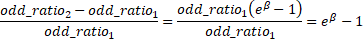
Therefore, each coefficient of the independent variable ways that for a unit change in the independent variable, the fractional increment in the odd ratio is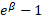 
(or the pct increase in the odd ratio is 
)
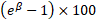Assuming our dependent variable is categorical and that 1 ways success and 0 means failure, the coefficients would accept been interpreted every bit follows:
- Holding all other factors constant, the pct increase in the odd of success is
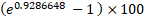(=153.eleven%) for a unit increase in 
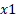. - Holding all other factors constant, the pct subtract in the odd of success is
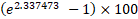(=935.5%) for a unit increase in 
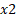(this is considering the sign of the coefficient is negative). - Holding all other factors abiding, the percentage increase in the odd of success is
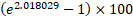(=652.35%) for a unit increase in 
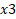. Since 
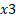is a categorical variable, assuming 0 represents female person while 1 correspond male; a unit increase in 
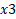is same equally switch from female (0) to male (1). We tin can thus say that the percentage increase in the odd of success is 652.35% for every unit of measurement switching from female gender to male or improve still; we can say that property all other factor abiding, the increment in the odd ratio of success we would expect for male is 652.35% that of female. - Property all other factors constant, the percent increase in the odd ratio of success is
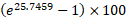(=51.8 
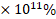) when all the independent variables each accept a value of zero.
Std. Err. is the standard error of the estimated parameters. It is a measured of the deviation we would expect for each of the parameter.
t is the t-statistics of the estimated parameters. Information technology is the ratio of coef to the std.Err. It measures how many times is the difference between the estimated coef and zero is greater than the std. Err.
P>|t| is the p-value associated with the t-statistics. It is the probability of obtaining the coef or even more (or less if coef is negative) that is significantly different from zero. For a threshold of 0.05, we have enough evidence to accept the alternate hypothesis that the estimated coefficients of x1, x2 and the intercept are not equal to 0 because their p-values are all bottom than 0.05. However, we cannot reject the nix hypothesis for x3 considering the its p-value is greater than the 0.05 significant threshold.
[95% Conf. Interval] is the 95% conviction interval. It gives the lower and upper boundaries in which we would expect to have coef to exist between 95% of the time.
Decision
We accept seen how to translate the regression output in Stata. The regression output of Stata can exist categorized into ANOVA table, model fit, and parameter interpretation. The estimation depends on the type of data of a particular variable.
See Also: Hypothesis Testing, Importance of Information Visualization, Linear Regression Simplified, Logistic Regression Explained, Understanding the Confusion Matrix
← Back
Source: https://www.academicianhelp.com/blog/regression-analysis-interpreting-stata-output
0 Response to "How to Read Linear Linear Stata Regression Output"
Publicar un comentario